TomSym compared to the Symbolic Toolbox

A hydroelectric dam.

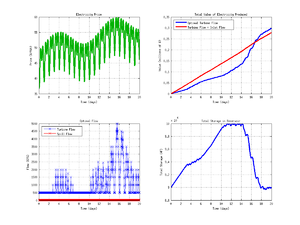
We look at the optimization problem of maximizing the revenue of a hydroelectric dam. This problem was published by By Seth DeLand of the MathWorks, as an example of how to combine their optimization and symbolic toolboxes. [1] We solve the same probem using tomSym and the TOMLAB solvers, noting a XXX times speed up. The problem can be solved in seconds with TOMLAB, as compared to hours with the MathWork's toolboxes.

The dynamics of the dam is described by the following equations.

Electricity(t) = TurbineFlow(t-1)*[½ k1(Storage(t) + Storage(t-1)) + k2]

Storage(t) = Storage(t-1) + ∆t * [inFlow(t-1) - spillFlow(t-1) - turbineFlow(t-1)]

The problem is to maximize revenue (electricity times price), subject to the following constraints:

• 0 < Turbine Flow < 25,000 CFS
• 0 < Spill Flow
• Max change in Turbine and Spill Flow < 500 CFS
• Combined Turbine and Spill Flow > 500 CFS
• 50000 < Reservoir Storage < 100000 Acre-Feet
• The final reservoir level must equal the initial level (90000 AF)

The actual data used by DeLand can be downloaded from Matlab Central.[2] To avoid attaching data files to our example, we will use an approximation to this data, as generated by the following Matlab code:

N = 480;
t = (0:N-1)';
inFlow = reshape(repmat(10*(107+[0 0 0 -3 3 2 2 -8 9 5 0 1 -6 -4 5 0 -6 -6 -17 -7]),24,1),N,1);
price = 46 + t./57 - 3*cos((t+46)/43) - 4*sin(pi/12*(t+4)) - 4*sin(pi/6*(t+1));

(The timing tests were run using both the original and the approximated data. Changes in indata has random effects on the number of iterations needed for convergence, but the effects are much smaller than the systematic differences between solvers.)

A few other consants are defined by DeLand as follows:

stor0 = 90000; % initial vol. of water stored in the reservoir (Acre-Feet)

k1 = 0.00003; % K-factor coefficient
k2 = 9; % K-factor offset

MW2kW = 1000; % MW to kW
C2A = 1.98347/24; % Convert from CFS to AF/HR

One the input data is defined, this is the entire code used to set up and solve the problem with TOMLAB:

turbineFlow = tom('turbineFlow',N,1);
spillFlow = tom('spillFlow',N,1);

outFlow = turbineFlow + spillFlow;

storage = stor0 + C2A*cumsum(inFlow - outFlow);

electricity = turbineFlow.*(0.5*k1*(storage + [stor0; storage(1:end-1)]) + k2)./MW2kW;

revenue = price*electricity; 

objective = -revenue; % Minimization objective

constraints = {
    0 <= turbineFlow <= 25000
    0 <= spillFlow
    -500 <= diff(outFlow) <= 500
    outFlow >= 500
    50000 <= storage <= 100000
    storage(end) == stor0
    };

guess = [];
 
options = struct;
options.solver = 'snopt';

solution = ezsolve(objective, constraints, guess, options);

Plots of the result, when the approximate indata is used.

The above code passes the same Hessian to the solver as DeLand's code. It is possible to get a much sparser Hessian, by making the water level a decision variable, instead of a symbolic expression. All we need to do is to replace the previous expression for "storage" by a symbol definition:

    storage = tom('storage',N,1);

and then add one constraint

    constraints{end+1} = ( storage == [stor0; storage(1:N-1)] + inFlow - outFlow );