PROPT The Brachistochrone Problem (DAE formulation): Difference between revisions
No edit summary |
No edit summary |
||
| Line 8: | Line 8: | ||
<math> E_{kin} = \frac{m}{2} \left( \frac{dx}{dt}^2 + \frac{dx}{dt}^2 \right) ,</math> | <math> E_{kin} = \frac{m}{2} \left( \frac{dx}{dt}^2 + \frac{dx}{dt}^2 \right) ,</math> | ||
<math> E_{pot} = m g y .</math> | <math> E_{pot} = m g y .</math> | ||
The boundary conditions are still A = (0,0), B = (10,-3), and an initial speed of zero, so we have | The boundary conditions are still A = (0,0), B = (10,-3), and an initial speed of zero, so we have | ||
<math> E_{kin} + E_{pot} = 0 </math> | <math> E_{kin} + E_{pot} = 0 </math> | ||
For complex mechanical systems, this freedom to choose the most convenient formulation can save a lot of effort in modelling the system. On the other hand, computation times may get longer, because the problem can to become more non-linear and the jacobian less sparse. | For complex mechanical systems, this freedom to choose the most convenient formulation can save a lot of effort in modelling the system. On the other hand, computation times may get longer, because the problem can to become more non-linear and the jacobian less sparse. | ||
Revision as of 08:06, 9 November 2011
|
This page is part of the PROPT Manual. See PROPT Manual. |
We will now solve the same problem as in brachistochrone.m, but using a DAE formulation for the mechanics.
DAE formulation
In a DAE formulation we don't need to formulate explicit equations for the time-derivatives of each state. Instead we can, for example, formulate the conservation of energy.
The boundary conditions are still A = (0,0), B = (10,-3), and an initial speed of zero, so we have
For complex mechanical systems, this freedom to choose the most convenient formulation can save a lot of effort in modelling the system. On the other hand, computation times may get longer, because the problem can to become more non-linear and the jacobian less sparse.
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.Problem setup
toms t
toms t_f
p = tomPhase('p', t, 0, t_f, 20);
setPhase(p);
tomStates x y
% Initial guess
x0 = {t_f == 10};
% Box constraints
cbox = {0.1 <= t_f <= 100};
% Boundary constraints
cbnd = {initial({x == 0; y == 0})
final({x == 10; y == -3})};
% Expressions for kinetic and potential energy
m = 1;
g = 9.81;
Ekin = 0.5*m*(dot(x).^2+dot(y).^2);
Epot = m*g*y;
v = sqrt(2/m*Ekin);
% ODEs and path constraints
ceq = collocate(Ekin + Epot == 0);
% Objective
objective = t_f;Solve the problem
options = struct;
options.name = 'Brachistochrone-DAE';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
x = subs(collocate(x),solution);
y = subs(collocate(y),solution);
v = subs(collocate(v),solution);
t = subs(collocate(t),solution);Problem type appears to be: lpcon
Time for symbolic processing: 0.10508 seconds
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - TOMLAB Development license 999007. Valid to 2011-12-31
=====================================================================================
Problem: --- 1: Brachistochrone-DAE f_k 1.869963310229926000
sum(|constr|) 0.000000000033224911
f(x_k) + sum(|constr|) 1.869963310263151000
f(x_0) 10.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 168 ConJacEv 168 Iter 93 MinorIter 156
CPU time: 0.062400 sec. Elapsed time: 0.071000 sec.
Plot the result
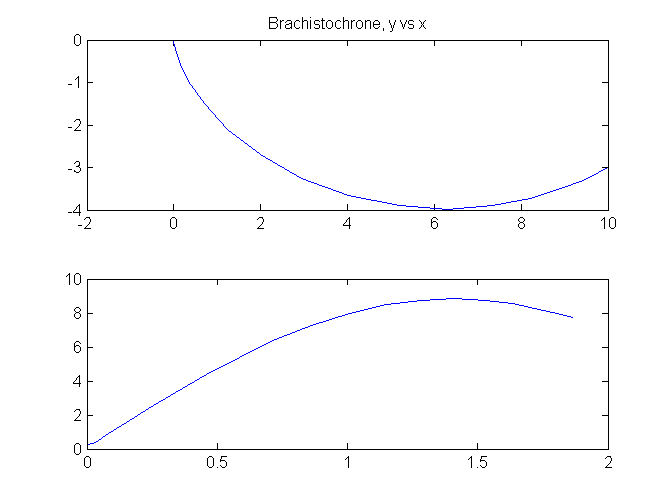
To obtain the brachistochrone curve, we plot y versus x.
subplot(2,1,1)
plot(x, y);
title('Brachistochrone, y vs x');
subplot(2,1,2)
plot(t, v);