PROPT The Brachistochrone Problem: Difference between revisions
From TomWiki
Jump to navigationJump to search
(Created page with " This problem was formulated by Johann Bernoulli, in Acta Eruditorum, June 1696 ==Problem description== "Given two points A and B in a vertical plane, what is the curve traced ...") |
No edit summary |
||
| (4 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
{{Part Of Manual|title=the PROPT Manual|link=[[PROPT|PROPT Manual]]}} | |||
This problem was formulated by Johann Bernoulli, in Acta Eruditorum, June 1696 | This problem was formulated by Johann Bernoulli, in Acta Eruditorum, June 1696 | ||
| Line 11: | Line 12: | ||
<math> \frac{dx}{dt} = v \sin(\theta) </math> | <math> \frac{dx}{dt} = v \sin(\theta) </math> | ||
<math> \frac{dy}{dt} = -v \cos(\theta) </math> | <math> \frac{dy}{dt} = -v \cos(\theta) </math> | ||
<math> \frac{dv}{dt} = g \cos(\theta) </math> | <math> \frac{dv}{dt} = g \cos(\theta) </math> | ||
where (x,y) is the coordinates of the point, v is the velocity, and theta is the angle between the direction of movement and the vertical. | where (x,y) is the coordinates of the point, v is the velocity, and theta is the angle between the direction of movement and the vertical. | ||
< | <source lang="matlab"> | ||
% Copyright (c) 2007-2009 by Tomlab Optimization Inc. | % Copyright (c) 2007-2009 by Tomlab Optimization Inc. | ||
</ | </source> | ||
==Problem setup== | ==Problem setup== | ||
< | <source lang="matlab"> | ||
toms t | toms t | ||
toms t_f | toms t_f | ||
| Line 59: | Line 63: | ||
% Objective | % Objective | ||
objective = t_f; | objective = t_f; | ||
</ | </source> | ||
==Solve the problem== | ==Solve the problem== | ||
< | <source lang="matlab"> | ||
options = struct; | options = struct; | ||
options.name = 'Brachistochrone'; | options.name = 'Brachistochrone'; | ||
| Line 72: | Line 76: | ||
theta = subs(collocate(theta),solution); | theta = subs(collocate(theta),solution); | ||
t = subs(collocate(t),solution); | t = subs(collocate(t),solution); | ||
</ | </source> | ||
<pre> | <pre> | ||
Problem type appears to be: lpcon | Problem type appears to be: lpcon | ||
Time for symbolic processing: 0. | Time for symbolic processing: 0.1296 seconds | ||
Starting numeric solver | Starting numeric solver | ||
===== * * * =================================================================== * * * | ===== * * * =================================================================== * * * | ||
| Line 91: | Line 95: | ||
FuncEv 1 ConstrEv 834 ConJacEv 834 Iter 224 MinorIter 826 | FuncEv 1 ConstrEv 834 ConJacEv 834 Iter 224 MinorIter 826 | ||
CPU time: 0. | CPU time: 0.436803 sec. Elapsed time: 0.446000 sec. | ||
</pre> | </pre> | ||
| Line 99: | Line 103: | ||
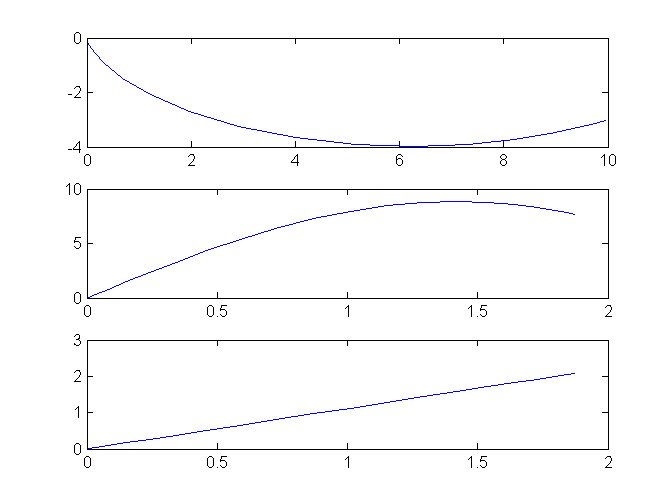
To obtain the brachistochrone curve, we plot y versus x. | To obtain the brachistochrone curve, we plot y versus x. | ||
< | <source lang="matlab"> | ||
subplot(3,1,1) | subplot(3,1,1) | ||
plot(x, y); | plot(x, y); | ||
| Line 109: | Line 113: | ||
subplot(3,1,3) | subplot(3,1,3) | ||
plot(t, theta) | plot(t, theta) | ||
</ | </source> | ||
[[File:brachistochrone_01.png]] | |||
[[Category:PROPT Examples]] | |||
Latest revision as of 04:52, 14 February 2012
|
This page is part of the PROPT Manual. See PROPT Manual. |
This problem was formulated by Johann Bernoulli, in Acta Eruditorum, June 1696
Problem description
"Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time."
In this example, we solve the problem numerically for A = (0,0) and B = (10,-3), and an initial speed of zero.
The mechanical system is modelled as follows:
where (x,y) is the coordinates of the point, v is the velocity, and theta is the angle between the direction of movement and the vertical.
% Copyright (c) 2007-2009 by Tomlab Optimization Inc.Problem setup
toms t
toms t_f
p = tomPhase('p', t, 0, t_f, 20);
setPhase(p);
tomStates x y v
tomControls theta
% Initial guess
% Note: The guess for t_f must appear in the list before expression involving t.
x0 = {t_f == 10
icollocate({
v == t
x == v*t/2
y == -1
})
collocate(theta==0.1)};
% Box constraints
cbox = {0.1 <= t_f <= 100
0 <= icollocate(v)
0 <= collocate(theta) <= pi};
% Boundary constraints
cbnd = {initial({x == 0; y == 0; v == 0})
final({x == 10; y == -3})};
% ODEs and path constraints
g = 9.81;
ceq = collocate({
dot(x) == v.*sin(theta)
dot(y) == -v.*cos(theta)
dot(v) == g*cos(theta)});
% Objective
objective = t_f;Solve the problem
options = struct;
options.name = 'Brachistochrone';
solution = ezsolve(objective, {cbox, cbnd, ceq}, x0, options);
x = subs(collocate(x),solution);
y = subs(collocate(y),solution);
v = subs(collocate(v),solution);
theta = subs(collocate(theta),solution);
t = subs(collocate(t),solution);Problem type appears to be: lpcon
Time for symbolic processing: 0.1296 seconds
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - TOMLAB Development license 999007. Valid to 2011-12-31
=====================================================================================
Problem: --- 1: Brachistochrone f_k 1.878940329113842700
sum(|constr|) 0.000000174716299412
f(x_k) + sum(|constr|) 1.878940503830142100
f(x_0) 10.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 834 ConJacEv 834 Iter 224 MinorIter 826
CPU time: 0.436803 sec. Elapsed time: 0.446000 sec.
Plot the result
To obtain the brachistochrone curve, we plot y versus x.
subplot(3,1,1)
plot(x, y);
subplot(3,1,2)
plot(t, v);
% We can also plot theta vs. t.
subplot(3,1,3)
plot(t, theta)