PROPT Drug Displacement Problem: Difference between revisions
From TomWiki
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 12: | Line 12: | ||
<math> J = t_F </math> | <math> J = t_F </math> | ||
subject to: | subject to: | ||
<math> \frac{dx_1}{dt} = g_1*(g_4*(0.02-x_1)+46.4*x_1*(u-2*x_2)) </math> | <math> \frac{dx_1}{dt} = g_1*(g_4*(0.02-x_1)+46.4*x_1*(u-2*x_2)) </math> | ||
<math> \frac{dx_2}{dt} = g_1*(g_3*(u-2*x_2)+46.4*(0.02-x_1)) </math> | <math> \frac{dx_2}{dt} = g_1*(g_3*(u-2*x_2)+46.4*(0.02-x_1)) </math> | ||
<math> g_2 = 1+0.2*(x_1+x_2) </math> | <math> g_2 = 1+0.2*(x_1+x_2) </math> | ||
<math> g_3 = g_2^2+232+46.4*x_2 </math> | <math> g_3 = g_2^2+232+46.4*x_2 </math> | ||
<math> g_4 = g_2^2+232+46.4*x_1 </math> | <math> g_4 = g_2^2+232+46.4*x_1 </math> | ||
<math> g_1 = \frac{g_2^2}{g_3*g_4-2152.96*x_1*x_2} </math> | <math> g_1 = \frac{g_2^2}{g_3*g_4-2152.96*x_1*x_2} </math> | ||
<math> 0 <= u <= 8 </math> | <math> 0 <= u <= 8 </math> | ||
x1 is the concentration of warfarin, and x2 of phenylbutazone. The initial and final condition are: | x1 is the concentration of warfarin, and x2 of phenylbutazone. The initial and final condition are: | ||
<math> x_0 = [0.02 \ 0] </math> | <math> x_0 = [0.02 \ 0] </math> | ||
<math> x_{t_f} = [0.02 \ 2.00] </math> | <math> x_{t_f} = [0.02 \ 2.00] </math> | ||
<source lang="matlab"> | <source lang="matlab"> | ||
Revision as of 08:07, 9 November 2011
|
This page is part of the PROPT Manual. See PROPT Manual. |
ITERATIVE DYNAMIC PROGRAMMING, REIN LUUS
12.4.3 Example 3: The desired level of two drugs, warfarin and phenylbutazone, must be reached in a patients bloodstream in minimum time.
CHAPMAN & HALL/CRC Monographs and Surveys in Pure and Applied Mathematics
Problem Formulation
Find u over t in [0; t ] to minimize
subject to:
x1 is the concentration of warfarin, and x2 of phenylbutazone. The initial and final condition are:
% Copyright (c) 2007-2008 by Tomlab Optimization Inc.Problem setup
toms t
toms t_f
p = tomPhase('p', t, 0, t_f, 50);
setPhase(p);
tomStates x1 x2
tomControls u
% Initial guess
x0 = {t_f == 300
icollocate({
x1 == 0.02; x2 == 2*t/t_f})
collocate(u == 8-8*t/t_f)};
% Box constraints
cbox = { 1 <= t_f <= 500
0 <= collocate(u) <= 8};
% Boundary constraints
cbnd = {initial({x1 == 0.02; x2 == 0})
final({x1 == 0.02; x2 == 2})};
% General variables
g2 = 1+0.2*(x1+x2);
g3 = g2.^2+232+46.4*x2;
g4 = g2.^2+232+46.4*x1;
g1 = g2.^2./(g3.*g4-2152.96*x1.*x2);
% ODEs and path constraints
ceq = collocate({
dot(x1) == g1.*(g4.*(0.02-x1)+46.4*x1.*(u-2*x2))
dot(x2) == g1.*(g3.*(u-2*x2)+46.4*(0.02-x1))});Solve the problem
options = struct;
options.name = 'Drug Displacement';
% Objective is first parameter
solution = ezsolve(t_f, {cbox, cbnd, ceq}, x0, options);
t = subs(collocate(t),solution);
u = subs(collocate(u),solution);Problem type appears to be: lpcon
Time for symbolic processing: 0.41796 seconds
Starting numeric solver
===== * * * =================================================================== * * *
TOMLAB - TOMLAB Development license 999007. Valid to 2011-12-31
=====================================================================================
Problem: --- 1: Drug Displacement f_k 221.333418113505790000
sum(|constr|) 0.000000061270786413
f(x_k) + sum(|constr|) 221.333418174776570000
f(x_0) 300.000000000000000000
Solver: snopt. EXIT=0. INFORM=1.
SNOPT 7.2-5 NLP code
Optimality conditions satisfied
FuncEv 1 ConstrEv 14 ConJacEv 14 Iter 10 MinorIter 256
CPU time: 0.046800 sec. Elapsed time: 0.048000 sec.
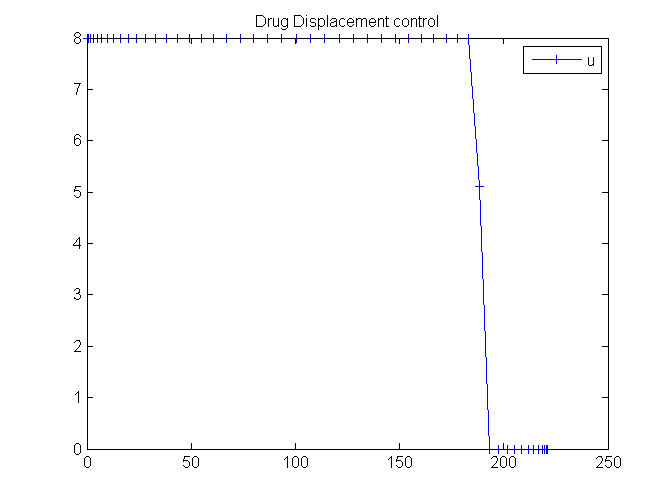
Plot result
figure(1)
plot(t,u,'+-');
legend('u');
title('Drug Displacement control');







![{\displaystyle x_{0}=[0.02\ 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08b69a8cd646e32764ae614ed6c4b64814a37c85)
![{\displaystyle x_{t_{f}}=[0.02\ 2.00]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1122af22fe09c9e15f04699b7d9f9ab717a0679f)